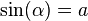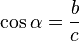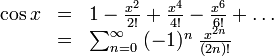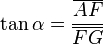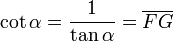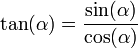viernes, 24 de febrero de 2012

Operaciones con matrices
Suma y Resta de matrices
Dadas dos matrices de la misma dimensión, A=(aij) y B=(bij), se define la matriz suma como: A+B=(aij+bij). Es decir, aquella matriz cuyos elementos se obtienen: sumando los elementos de las dos matrices que ocupan la misma misma posición.
  Sea A = 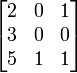 \begin{bmatrix} 2 & 0 & 1\\ 3 & 0 & 0 \\5 &1& 1 \end{bmatrix} 

 y B = 

\begin{bmatrix} 1 & 0 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 0 \end{bmatrix} 



 La suma A + B


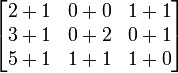
\begin{bmatrix} 2+1 & 0+0 & 1+1  \\ 3+1 &0 +2 & 0+1\\5+1&1+1 &1+0  \end{bmatrix} 

es igual  a
\begin{bmatrix} 3 & 0& 2 \\ 4& 2 &1 \\ 6 & 2& 1 \end{bmatrix}
Del mismo modo la resta se hace componente a componente A - B




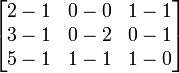
\begin{bmatrix} 2-1 & 0-0 & 1-1  \\ 3-1 &0 -2 & 0-1\\5-1&1-1 &1-0  \end{bmatrix}
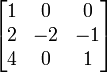
es igual a \begin{bmatrix} 1&0&0\\2&-2&-1\\4&0&1 \end{bmatrix}


 Propiedades de la suma de matrices

De la dimension

La suma de dos matrices de orden m x n es otra matriz dimensión m x n.

 Asociativa

A + (B + C) = (A + B) + C

 Elemento neutro

A + 0 = A Donde O es la matriz nula de la misma dimensión que la matriz A.

\Elemento opuesto

A + (-A) = O La matriz opuesta es aquella en que todos los elementos están cambiados de signo.

 Conmutativa

A + B = B + A

 Producto de matrices

Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B. Mm x n x Mn x p = M m x p El elemento cij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos. A•B =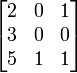 \begin{bmatrix} 2 & 0 & 1\\ 3 & 0 & 0 \\5 &1& 1 \end{bmatrix} • \begin{bmatrix} 1 & 0 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 0 \end{bmatrix}
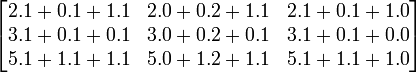\begin{bmatrix} 2.1+0.1+1.1 & 2.0+0.2+1.1 & 2.1+0.1+1.0 \\ 3.1+0.1+0.1& 3.0+0.2+0.1& 3.1+0.1+0.0\\5.1+1.1+1.1&5.0+1.2+1.1 &5.1+1.1+1.0\end{bmatrix} es igual a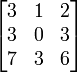
\begin{bmatrix} 3 & 1 & 2\\ 3 & 0 & 3 \\7 &3& 6 \end{bmatrix}




 Propiedades del producto de matrices

Asociativa

A • (B • C) = (A • B) • C

 Elemento neutro

A • I = A Donde I es la matriz identidad del mismo orden que la matriz A. Anticonmutativa A • B ≠ B • A

 Distributiva del producto respecto de la suma

 Matriz inversa

A · A-1 = A-1 · A = I


Propiedades

(A · B)-1 = B-1 · A-1 (A-1)-1 = A (k · A)-1 = k-1 · A-1 (A t)-1 = (A -1)t


 Cálculo de la inversa por el método de Gauss

Sea A una matriz cuadrada de orden n. Para calcular la matriz inversa de A, que denotaremos como A-1, seguiremos los siguientes pasos: 1º Construir una matriz del tipo M = (A | I), es decir, A está en la mitad izquierda de M y la matriz identidad I en la derecha. Consideremos una matriz 3x3 arbitraria
La ampliamos con la matriz identidad de orden 3.
2º Utilizando el método Gauss vamos a transformar la mitad izquierda, A, en la matriz identidad, que ahora está a la derecha, y la matriz que resulte en el lado derecho será la matriz inversa: A-1. F2 - F1

F3 + F2

F2 - F3

F1 + F2

(-1) F2

La matriz inversa es: F1


Puedes consultar este otro método para calcular la matriz inversa.
A • (B + C) = A • B + A • C
Publicado por en No hay comentarios:
Funciones:

Funciones Radicales:
La función raíz n-ésima (leáse "raíz ene-ésima") es la función inversa de la función elemental de potenciación. Y en tanto que inversa de un tipo de función elemental la función raíz es también una función elemental. Si en una función, la variable independiente esta bajo el signo de radicación, sin poder obtener una expresión de esa misma función en la que no este, esa función es irracional, por ejemplo:
y =\sqrt{x}
Si tenemos la función:
y = \sqrt{x^2 +2x +1}
la variable independiente, x, esta bajo el signo de radicación, pero podemos ver que:
y= \sqrt{x^2+2x+1} \rightarrow \quad y= \sqrt{(x+1)^2} \rightarrow \quad y= x+1
con lo que obtenemos una función no irracional.

Funcion cubica:
La función cúbica es una función polinómica de tercer grado. Tiene la forma:

f(x) = ax^3 + bx^2 + cx + d \, ; donde el coeficiente a es distinto de 0.
Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales.
La derivada de una función cúbica genera una función cuadrática y su integral una función cuártica.

Funcion exponencial:
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:
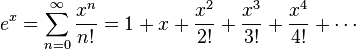
e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots
o como el límite de la sucesión:
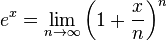
e^x = \lim_{n \to \infty} \left( 1 + {x \over n} \right)^n


Funcion Racional:
En matemáticas, una función racional es una función que puede ser expresada de la forma:
f(x) = \frac{P(x)}{Q(x)}
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.[1]
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Funciones Logaritmicas
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo b (base) se ha de elevar para obtener dicho argumento. Es la función inversa de b a la potencia n. Esta función se escribe como: n = logb x, lo que permite obtener n.[1]
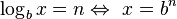
\log_b x = n\Leftrightarrow\ x = b^n\,
(esto se lee como: logaritmo en base "b" de "x" es igual a "n"; sí y sólo si "b" elevado a la "n" da por resultado a "x")
  • La base b tiene que ser positiva y distinta de 1 (b>0, b \ne 1)\,.
  • x tiene que ser un número positivo (x>0)\,.
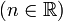  • n puede ser cualquier número real (n\in\mathbb{R})\,.
Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.

Funciones trigonometricas

Seno

    
Trigono b00.svg
En trigonometría el seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la Hipotenusa:
\sin(\alpha)=\frac{a}{c}
O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c=1):
\sin(\alpha)=a \,

Coseno

Trigono b00.svg
En trigonometría el coseno (abreviado cos) de un ángulo agudo en un triángulo rectángulo se define como la razón entre el cateto adyacente a ese ángulo y la hipotenusa:
\cos\alpha = \frac{b}{c}
En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo α.
Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la circunferencia goniométrica, es decir, la circunferencia unitaria centrada en el origen. En este caso el valor del coseno coincide con la abscisa del punto de intersección del ángulo con la circunferencia. Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.
En análisis matemático el coseno es la función que asocia un número real x con el valor del coseno del ángulo de amplitud, expresada en radianes, x. Es una función trascendente y analítica, cuya expresión en serie de potencias es
\begin{array}{rcl} \cos x & = & 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \\ & = & \sum_{n=0}^\infty \; (-1)^n \; \frac{x^{2n}}{(2n)!} \end{array}
La serie de potencias anterior proporciona a su vez la extensión de la función coseno al plano complejo del siguiente modo:
{\rm cos\ }z=\frac{e^{iz} + e^{-iz} }{2}
Donde i es la unidad imaginaria.

Cotangente
Trigono d00.svg

Partiendo del triángulo AGF rectángulo en F, como ya se ha dicho, tenemos que:
\tan \alpha = \frac{\overline{AF}}{\overline{FG}}


Donde el segmento AF vale uno:
\tan \alpha = \frac{1}{\overline{FG}}
Con lo que resulta:
\cot \alpha = \frac{1}{\tan \alpha} = \overline{FG}
Tangente
En trigonometría la tangente de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y el adyacente:
\tan(\alpha) = \frac{a}{b}
O también como la relación entre el seno y el coseno:
\tan(\alpha) = \frac{\sin(\alpha) }{\cos(\alpha) } \,
Secante
La Secante, (abreviado como sec), es la razón trigonométrica inversa del coseno, o también su inverso multiplicativo:
\sec \alpha = \frac{1}{\cos \alpha} = \frac{c}{b}
Cosecante
La Cosecante (abreviado como csc o cosec) es la razón trigonométrica inversa del seno, o también su inverso multiplicativo:
\csc \alpha = \frac{1}{\operatorname {sen} \alpha} = \frac{c}{a}
Valor Absoluto
En matemática, el valor absoluto o módulo de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.
Publicado por en No hay comentarios:
FUNCION EXPLICITA

Una función es explicita cuando en la ecuación que actúa como regla de correspondencia ,se tiene despejada la variable dependiente y términos de la variable independiente x.

La función y=f(x)=3x2 +2x+1 es una función explicita ,dado que la ecuación ,es la regla de correspondencia ,permite calcular directamente para cualquier valor “x” del dominio, su imagen correspondiente “y”en el contradominio.


FUNCION IMPLÍCITA

Considérese ahora a f(x,y)como representación de una expresión en x, y;en tal forma que f(x,y)=0..(1)es una ecuación en x,y no resuelta para y

La ecuación 2x2 –2xy+y2 -1=0..(a)

Es una ecuación del tipof(x,y)=0...(1)

Donde f(x,y)=2x2-2x+y2-1

Se despeja la ecuación en este caso de segundo grado en “y”

Y2-2xy+(2x2-1)=0

Donde



Y=2x±Ö4x2-4(2x2-1) =x±1/2Ö4-4x2

2

las soluciones de dicha ecuación son y=x±Ö1-x2


dado que hay dos valores de “y” para cada valor de “x” en el intervalo abierto(-1,1),

la ecuación (a) especifica una relación multiforme ,pero no una función.

Una función implícita se caracteriza porque en la ecuación que actúa como regla de correspondencia ,la variable dependiente y no se encuentra despejada .
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)